En este artículo explicaremos
- cómo funcionan las loterías
- cómo generan beneficios las loterías
- qué posibilidades tiene de ganar un premio concreto en la lotería
- cómo funcionan las matemáticas detrás de la lotería
- el concepto de expectativa de ganancia, también conocido como Valor Esperado
- cómo tener en cuenta todos estos factores para decidir a qué lotería jugar y cuándo comprar un boleto.
¿Cómo generan beneficios las loterías?
En pocas palabras, todas las loterías obtienen beneficios asegurándose de que sólo un porcentaje del dinero ingresado por la venta de boletos se pague en forma de premios. Para obtener beneficios, hay que tener en cuenta los pagos en todos los niveles de premios, desde el bote hasta el premio más pequeño posible.
La mayoría de las loterías estatales tienen márgenes relativamente altos. Las dos razones principales son:
- Sus gastos de explotación y administración son relativamente elevados.
- Sus beneficios se destinan a apoyar todo tipo de proyectos sociales u otras iniciativas de interés público. Puede tratarse de deportes de aficionados, proyectos medioambientales, etc. En lugar de utilizar los ingresos fiscales para financiar estos proyectos, los Estados suelen celebrar loterías para conseguir los fondos necesarios. Se podría incluso decir que las loterías son una forma de fiscalidad «voluntaria».
¿Qué posibilidades tienen los jugadores de ganar?
Veamos las matemáticas que hay detrás del concepto de lotería. En cada nivel ganador, sus posibilidades vienen definidas por el número de resultados posibles del sorteo, o las probabilidades. Estas probabilidades suelen ser de 1 en X, siendo X el número de resultados posibles. Pero dividiendo 1 entre X, también puede obtener esas probabilidades como porcentaje.
Por ejemplo, si tiras un dado, hay seis resultados posibles. Adivinar el resultado de cualquier tirada te daría una probabilidad de 1 entre 6. También puedes dividir 1 entre 6, y obtendrás un 16,667% de posibilidades de acertar el resultado.
Al mismo tiempo, también debe tener en cuenta la cantidad que puede ganar y el precio que paga por participar. Analicemos detenidamente este concepto.
El concepto de expectativa de beneficio o valor esperado
Permítame utilizar un ejemplo sencillo para explicar qué es el Valor Esperado. Utilizaremos aquí la abreviatura EV.
Supongamos que lanzo una moneda y le pago 1 $ cada vez que sale cara. Si hiciéramos esto muchas, muchas veces, el VE se acercaría a cero, ¿verdad?
Pero, ¿y si yo te pagara 2 $ cada vez que ganas y tú me pagaras 1 $ cada vez que pierdes? Bueno, eso significaría que a la larga obtendrías beneficios. Si tiras la moneda mil veces, el resultado sería aproximadamente 500 veces cara (ganas 1.000 $) y 500 veces cruz (pierdes 500 $). Es decir, un beneficio de 500 $ por cada 1.000 lanzamientos, o 0,50 $ por lanzamiento.
¿Cómo podemos aplicar esto a la lotería?
Suponiendo un precio fijo del billete (podemos utilizar 1 $ como precio de una participación en la lotería), tenemos que calcularlo de la siguiente manera:
El porcentaje de probabilidad, multiplicado por la cantidad que ganarías = Tu valor esperado
Si queremos saber cómo se aplica esto a ganar el premio gordo, así es como lo hacemos. Utilicemos Mega Millions como ejemplo. Las probabilidades de ganar el bote aquí son de 1 entre 302.575.350, lo que significa un porcentaje de 0,00000033049619%. El otro factor es el tamaño del bote, que por supuesto varía. La siguiente tabla muestra cómo su EV depende del tamaño del bote.Megamillions jackpot EV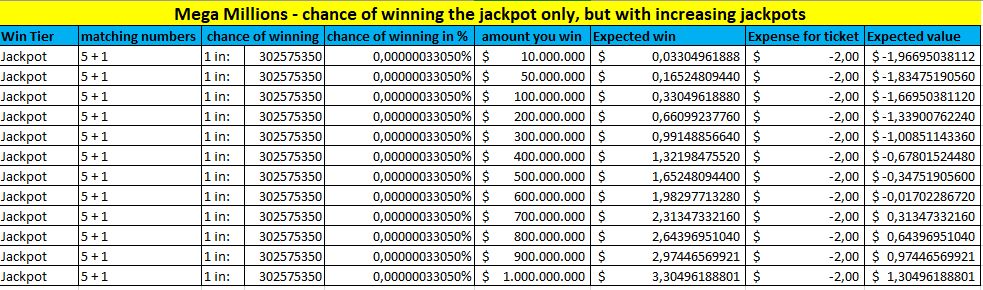
Esto es interesante, ¿verdad? Puede ver que, matemáticamente, su EV aumenta a medida que aumenta el bote. De hecho, en esa tabla, puede ver que cuando el bote es de 700 millones de dólares, su EV es de aproximadamente 0,31 dólares. Y este número ni siquiera tiene en cuenta sus posibilidades de ganar cualquiera de los otros premios en los niveles inferiores.
Esto nos lleva a otra reflexión interesante. Suponiendo que el bote sea de 700 millones de dólares y que haya 302,575 millones de combinaciones de números posibles. ¿Qué pasaría si tuviéramos que comprar 302.575 millones de boletos, al precio de 2,00 $, para cubrir todas las combinaciones de números posibles? Eso nos costaría unos 605 millones de dólares, pero tendríamos una ganancia garantizada de 700 millones de dólares más todas las ganancias menores. Eso debería funcionar, ¿verdad? Desafortunadamente, esto no funcionará, incluso si usted tuviera el dinero para comprar tantos billetes de lotería.
Entonces, ¿por qué no es una estrategia viable para ganar siempre?
Dos simples razones:
- Impuestos – si gana, tendrá que pagar al menos un 30% de impuestos sobre sus ganancias. Eso significa que el bote tiene que ser aún mayor de lo que sugiere la tabla, para que usted tenga un beneficio garantizado.
- Múltiples ganadores se repartirán el bote: puede que tenga garantizado ganar el bote, pero ¿qué ocurre si una o dos personas más tienen los números ganadores? Tendrías que dividir el bote, pero la cantidad que ganas no está garantizada. Además, está la cuestión fiscal.
Comparación del valor esperado de las mayores loterías
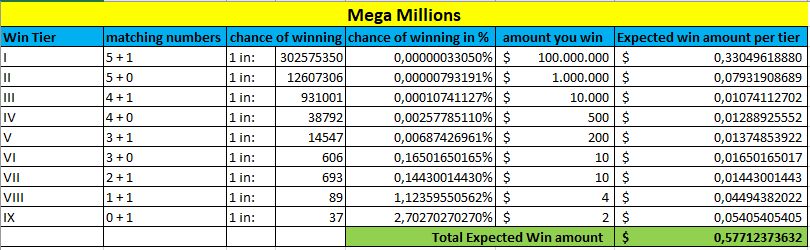
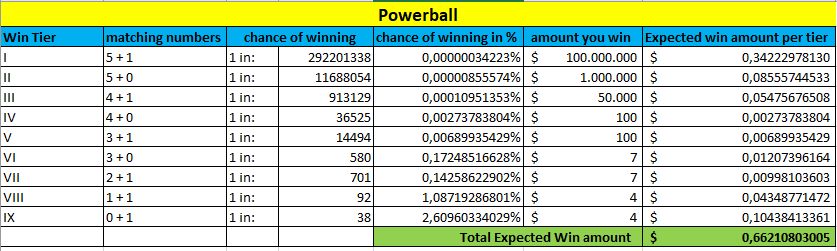
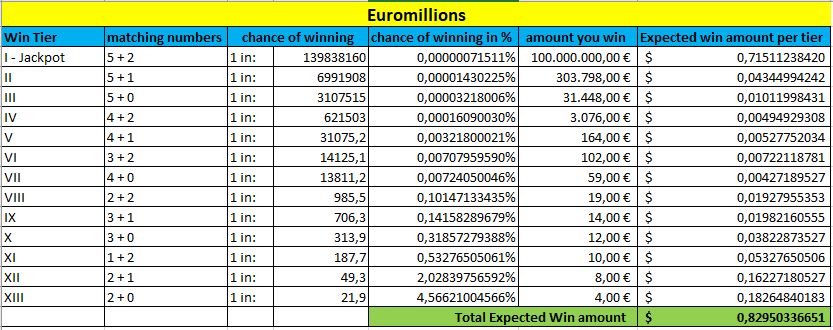
Ahora echaremos un vistazo a qué loterías ofrecen el «mejor trato» por su dinero. Compararemos las loterías más vendidas, que son Mega Millions, Powerball, Euromillones y Eurojackpot. Para poder ofrecer una comparación justa, supondremos que el bote es el mismo para cada lotería, de 100 millones.
Además, ahora tendremos en cuenta todos los niveles de premios y sus probabilidades, junto con la cantidad media que se puede esperar en cada nivel.
En la parte inferior de cada tabla, marcada en verde, puede ver la cantidad de Ganancia Esperada. Cuanto mayor sea este importe, mayores serán sus posibilidades de ganar esta lotería.
Mega Millones
Powerball
Euromillones
Eurojackpot
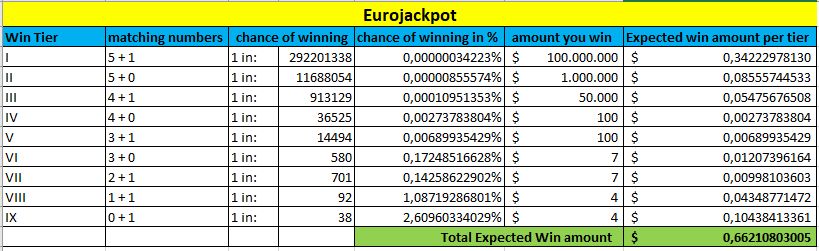
De nuevo, todo esto cambia cuando los botes aumentan. Pero la tabla anterior le ofrece una buena comparación de las loterías en general, basada en sus probabilidades de ganar cualquier premio.
Conclusión
No todas las loterías ofrecen las mismas probabilidades de ganar. Aunque las diferentes loterías funcionan básicamente de la misma manera, cada lotería tiene una estructura diferente de pagos y ganancias.
Pero al fin y al cabo, lo único que tiene sentido es que cuanto mayor sea el bote, ¡más razones tendrás para comprar un boleto y participar en la lotería!
