Dans cet article, nous allons expliquer
- comment fonctionnent les loteries
- comment les loteries génèrent des bénéfices
- quelles sont vos chances de gagner un prix spécifique à la loterie
- comment fonctionne le calcul mathématique de la loterie
- le concept d’espérance de gain, également connu sous le nom de valeur attendue
- comment prendre en compte tous ces facteurs pour décider à quelle loterie jouer et quand acheter un billet.
Comment les loteries génèrent-elles des bénéfices ?
En termes simples, toutes les loteries réalisent des bénéfices en s’assurant que seul un pourcentage de l’argent collecté par la vente des billets sera reversé sous forme de gains. Pour faire des bénéfices, il faut prendre en compte les paiements de tous les paliers de gains, du jackpot au plus petit gain possible.
La plupart des loteries publiques ont des marges relativement élevées. Les deux principales raisons en sont les suivantes :
- Leurs frais de fonctionnement et d’administration sont relativement élevés
- Leurs bénéfices sont utilisés pour soutenir toutes sortes de projets sociaux ou d’autres initiatives d’intérêt public. Il peut s’agir de sports amateurs, de projets environnementaux, etc. Au lieu d’utiliser les recettes fiscales pour financer ces projets, les États organisent souvent des loteries pour trouver les fonds nécessaires. On pourrait même dire que les loteries sont une forme d’imposition « volontaire ».
Quelles sont les chances de gain des joueurs ?
Examinons les mathématiques qui sous-tendent le concept de loterie. Pour chaque lot gagnant, vos chances sont définies par le nombre de résultats possibles du tirage, c’est-à-dire les probabilités. Ces chances sont souvent données comme étant de 1 sur X – X étant le nombre de résultats possibles. Mais en divisant 1 par X, vous pouvez également obtenir ces chances sous forme de pourcentage.
Par exemple, si vous lancez un dé, il y a six résultats possibles. En devinant le résultat d’un lancer, vous avez une chance sur six. Vous pouvez également diviser 1 par 6 et vous obtiendrez 16 667 % de chances de deviner le bon résultat.
Dans le même temps, vous devez également tenir compte du montant que vous pouvez gagner et du prix que vous payez pour participer. Examinons ce concept de plus près.
Le concept d’espérance de gain ou de valeur attendue
Permettez-moi d’utiliser un exemple simple pour expliquer ce qu’est la valeur attendue. Nous utiliserons ici l’abréviation EV.
Supposons que je joue à pile ou face et que je vous verse 1 $ chaque fois que le résultat est pile. Mais à chaque fois que le résultat est pile, vous devez me payer 1 $. Si nous devions faire cela un très grand nombre de fois, la VE se rapprocherait de zéro, n’est-ce pas ?
Mais que se passerait-il si je vous payais 2 dollars à chaque fois que vous gagnez et que vous me payiez 1 dollar à chaque fois que vous perdez ? Cela signifierait que vous réalisez un bénéfice à long terme. Si vous jouez mille fois à pile ou face, vous obtiendrez environ 500 fois pile (vous gagnez 1 000 $) et 500 fois face (vous perdez 500 $). Cela représente un bénéfice de 500 $ pour 1 000 tirages, soit 0,50 $ par tirage.
Comment appliquer ce principe à la loterie ?
En supposant que le prix du billet est fixe (nous pouvons utiliser 1 $ comme prix d’entrée à la loterie), nous devons le calculer comme suit :
Le pourcentage de chance, multiplié par le montant que vous gagneriez = Votre valeur attendue
Si nous voulons savoir comment cela s’applique au gain du jackpot, voici comment procéder. Prenons l’exemple de Mega Millions. Les chances de gagner le jackpot sont de 1 sur 302.575.350, soit un pourcentage de 0,00000033049619%. L’autre facteur est le montant du jackpot, qui varie bien entendu. Le tableau suivant montre comment votre EV dépend de la taille du jackpot.Megamillions jackpot EV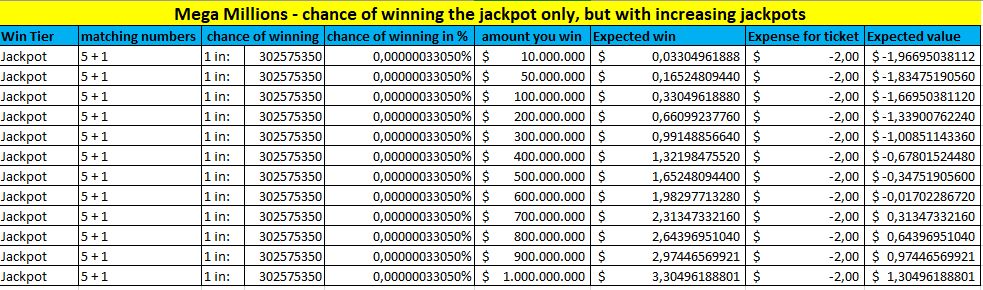
C’est intéressant, non ? Vous pouvez voir que, mathématiquement, votre EV augmente à mesure que le jackpot augmente. En fait, dans ce tableau, vous pouvez voir que lorsque le jackpot est de 700 millions de dollars, votre VE est d’environ 0,31 $. Et ce chiffre ne tient même pas compte de vos chances de gagner l’un des autres prix des paliers inférieurs.
Cela nous amène à une autre réflexion intéressante. Supposons que le jackpot s’élève à 700 millions de dollars et qu’il existe 302,575 millions de combinaisons de numéros possibles. Que se passerait-il si nous achetions 302 575 millions de billets, au prix de 2,00 $, pour couvrir toutes les combinaisons possibles ? Cela nous coûterait environ 605 millions de dollars, mais nous aurions un gain garanti de 700 millions de dollars, plus tous les petits gains. Cela devrait fonctionner, n’est-ce pas ? Malheureusement, cela ne fonctionnera pas, même si vous aviez l’argent nécessaire pour acheter autant de billets de loterie.
Pourquoi cette stratégie n’est-elle pas viable pour gagner à tous les coups ?
Pour deux raisons simples :
- Les impôts – si vous gagnez, vous devrez payer au moins 30 % d’impôts sur vos gains. Cela signifie que le jackpot doit être encore plus élevé que ce que le tableau suggère, pour que vous ayez un bénéfice garanti.
- Plusieurs gagnants se partageront le jackpot – vous êtes peut-être assuré de gagner le jackpot, mais que se passe-t-il si une ou deux autres personnes ont les numéros gagnants ? Vous devrez partager le jackpot, mais le montant que vous gagnez n’est pas garanti. Et puis, il y a encore la question de la fiscalité.
Comparaison de la valeur attendue des plus grandes loteries
Nous allons maintenant examiner quelles sont les loteries qui offrent le meilleur rapport qualité-prix. Nous allons comparer les loteries les plus vendues, à savoir Mega Millions, Powerball, Euromillions et Eurojackpot. Pour que la comparaison soit équitable, nous supposerons que le jackpot est le même pour chaque loterie, à savoir 100 millions.
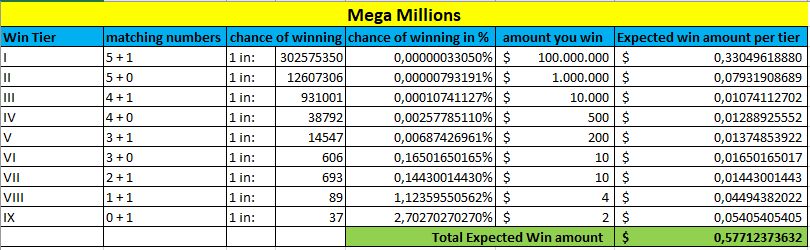
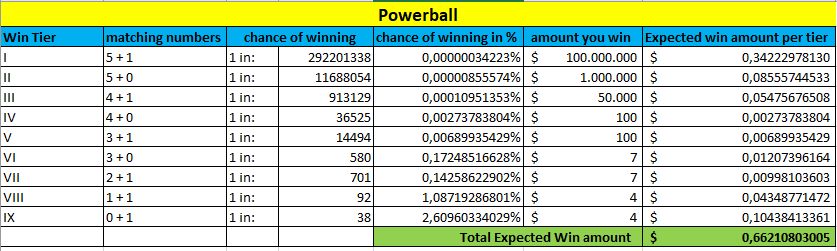
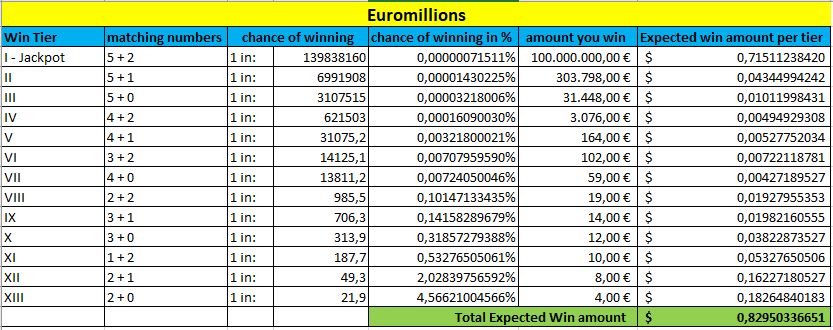
Nous prendrons également en compte tous les paliers de prix et leurs probabilités, ainsi que le montant moyen que vous pouvez espérer pour chaque palier.
En bas de chaque tableau, marqué en vert, vous pouvez voir le montant du gain attendu. Plus ce montant est élevé, plus vous avez de chances de gagner cette loterie.
Mega Millions
Powerball
Euromillions
Eurojackpot
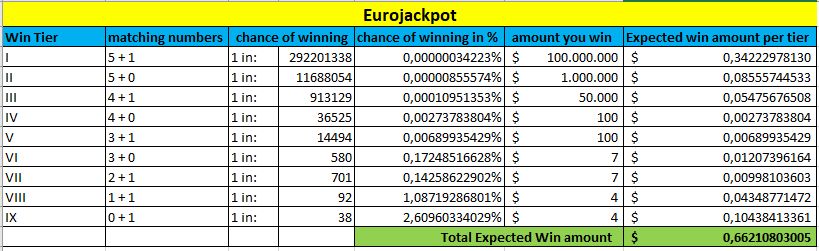
Encore une fois, tout cela change lorsque les jackpots augmentent. Mais le tableau ci-dessus vous donne une bonne comparaison des loteries en général, sur la base de vos chances de gagner un prix.
Conclusion
Toutes les loteries n’offrent pas les mêmes chances de gagner. Bien que les différentes loteries fonctionnent toutes de la même manière, chaque loterie a une structure différente de paiements et de gains.
Mais en fin de compte, ce qui est logique, c’est que plus le jackpot est élevé, plus vous avez de raisons d’acheter un billet et de participer à la loterie !
