U ovom članku ćemo objasniti:
- kako lutrije funkcioniraju
- kako lutrije ostvaruju profit
- koje su vaše šanse za osvajanje određene nagrade na lutriji
- kako matematika iza lutrije funkcionira
- koncept očekivanog profita, poznatog i kao Očekivana vrijednost
- kako uzeti u obzir sve te faktore kako biste odlučili koju lutriju igrati, i kada kupiti listić
Kako lutrije ostvaruju profit?
Jednostavno rečeno, sve lutrije ostvaruju profit osiguravajući da samo postotak novca koji dolazi od prodaje ulaznica bude isplaćen u obliku dobitaka. Da bi ostvarili profit, moraju se uzeti u obzir isplate u svim dobitnim razinama, od glavne do najmanje moguće nagrade.
Većina državnih lutrija ima relativno visoke marže. Dva glavna razloga za to su:
- Imaju relativno visoke operativne i administrativne troškove
- Njihov profit koristi se za podršku raznim projektima socijalne skrbi ili drugim nastojanjima koja su u javnom interesu. To mogu biti amaterski sportovi, ekološki projekti, itd. Umjesto korištenja poreznih prihoda za financiranje takvih projekata, države često organiziraju lutrije kako bi prikupile potrebna sredstva. Čak možete reći da su lutrije oblik “dobrovoljnog” oporezivanja.
Što određuje šanse za pobjedu igrača?
Pogledajmo matematiku iza koncepta lutrije. U svakoj dobitnoj razini, vaše šanse određene su brojem mogućih ishoda izvlačenja, odnosno šansama. Te šanse često se izražavaju kao 1 prema X – X je broj mogućih ishoda. Ali dijeljenjem 1 s X, možete dobiti te šanse i kao postotak.
Primjerice, ako bacite kocku, postoji šest mogućih ishoda. Pogađanje rezultata bilo kojeg bacanja dalo bi vam šansu od 1 prema 6. Također biste mogli podijeliti 1 s 6 i dobiti 16,667% šanse da pogodite pravi ishod.
Isto tako, trebate uzeti u obzir i iznos koji možete osvojiti, i cijenu koju plaćate za sudjelovanje. Pogledajmo bliže taj koncept.
Koncept očekivanog profita, ili Očekivane vrijednosti
Dopustite mi da upotrijebim jednostavan primjer kako biste shvatili što je Očekivana vrijednost. Ovdje ćemo koristiti kraticu OV.
Recimo da bacim novčić i platim vam 1 dolar svaki put kada rezultat bacanja novčića bude glava. Ali svaki put kad rezultat bude pismo, morate mi platiti 1 dolar. Ako bismo ovo radili mnogo puta, OV bi se približio nuli, zar ne?
Ali što ako bih vam platio 2 dolara svaki put kad pobijedite, a vi meni platite 1 dolar svaki put kad izgubite? Pa, to bi značilo da ostvarujete profit u dugoročnom smislu. Bacite novčić tisuću puta, rezultat bi bio približno 500 puta glava (osvojite 1000 dolara) i 500 puta pismo (izgubite 500 dolara). To je profit od 500 dolara za 1000 bacanja novčića, ili 0,50 dolara po bacanju novčića.
Kako to možemo primijeniti na lutriju?
Pretpostavimo fiksnu cijenu ulaznice (ovdje možemo koristiti 1 dolar kao cijenu za jedan ulazak u lutriju), moramo to izračunati na sljedeći način:
Postotak šanse, pomnožen s iznosom koji biste osvojili = Vaša očekivana vrijednost
Ako želimo znati kako se to odnosi na osvajanje glavne nagrade, to ćemo učiniti ovako. Koristimo Mega Millions kao primjer. Šanse za osvajanje glavne nagrade ovdje su 1 prema 302.575.350, što znači postotak od 0,00000033049619%. Drugi faktor je veličina glavne nagrade, koja naravno varira. Sljedeća tablica prikazuje kako vaša OV ovisi o veličini glavne nagrade.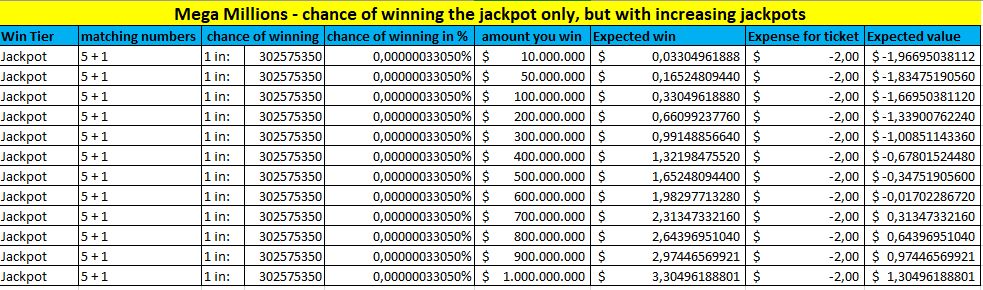
Ovo je zanimljivo, zar ne? Možete vidjeti da se matematički vaša OV povećava s povećanjem glavne nagrade. Zapravo, u toj tablici možete vidjeti da kada je glavna nagrada 700 milijuna dolara, vaša OV je približno 0,31 dolara. A ovaj broj čak ne uzima u obzir vaše šanse za osvajanje bilo koje druge nagrade u nižim razinama.
To nas dovodi do još jedne zanimljive misli. Pretpostavimo da je glavna nagrada 700 milijuna dolara, a postoji 302,575 milijuna mogućih kombinacija brojeva. Što ako bismo kupili 302,575 milijuna ulaznica, po cijeni od 2,00 dolara, kako bismo pokrili sve moguće kombinacije brojeva? To bi nas koštalo otprilike 605 milijuna dolara, ali imali bismo zajamčenu dobit od 700 milijuna dolara plus sve manje dobitke. To bi trebalo funkcionirati, zar ne? Nažalost, ovo neće funkcionirati, čak i ako imate novac za kupnju toliko mnogo lutrijskih ulaznica.
Zašto ovo nije održiva strategija za osvajanje svaki put?
Dva jednostavna razloga:
- Porezi – ako pobijedite, morat ćete platiti barem 30% poreza na svoje dobitke. To znači da glavna nagrada mora biti čak veća od onoga što tablica sugerira, kako biste ostvarili zajamčeni profit.
- Višestruki dobitnici podijelit će glavnu nagradu – možda ste zajamčeni osvajanje glavne nagrade, ali što ako još jedna ili dvije osobe imaju pobjedničke brojeve? Morat ćete podijeliti glavnu nagradu, ali iznos koji osvojite nije zajamčen. A onda tu je i pitanje poreza.
Usporedba očekivane vrijednosti za najveće lutrije
Sada ćemo pogledati koje lutrije nude “najbolji posao” za vaš novac. Usporedit ćemo naše najprodavanije lutrije, koje su Mega Millions, Powerball, Euromillions i Eurojackpot. Kako bismo pružili poštenu usporedbu, pretpostavit ćemo da je glavna nagrada ista za svaku lutriju, 100 milijuna.
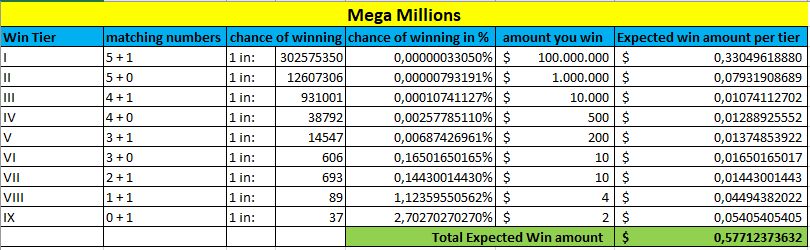
Također, sada ćemo uzeti u obzir sve razine nagrada i njihove vjerojatnosti, u kombinaciji s prosječnim iznosom koji možete očekivati u svakoj razini.
Na dnu svake tablice, označene zeleno, možete vidjeti iznos Očekivane dobiti. Što je taj iznos veći, to su vaše šanse bolje za osvajanje ove lutrije.
Mega Millions
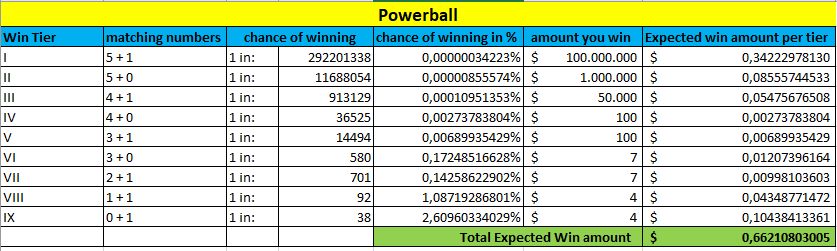
Powerball
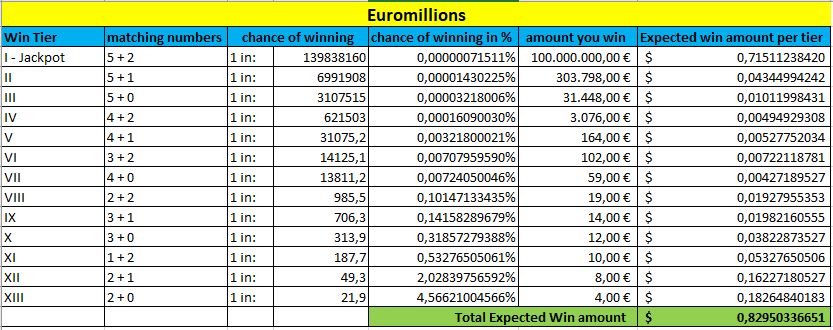
Euromillions
Eurojackpot
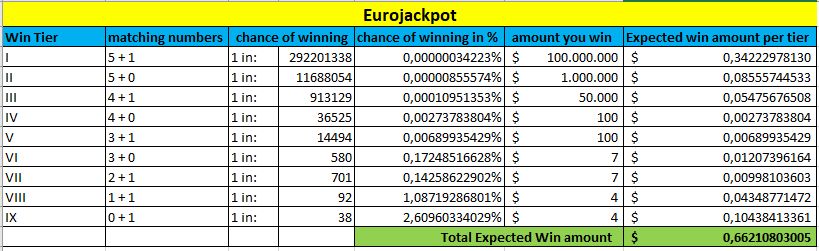
Ponovno, sve se to mijenja kada se povećavaju glavne nagrade. Ali gornja tablica daje vam dobru usporedbu lutrija općenito, na temelju vaših šansi za osvajanje bilo koje nagrade.
Zaključak
Sve lutrije ne nude iste šanse za osvajanje. Iako sve lutrije u osnovi funkcioniraju na isti način, svaka lutrija ima drugačiju strukturu isplata i dobitaka.
Ali na kraju dana, jedna stvar koja ima smisla je da što je veća glavna nagrada, više razloga imate da kupite listić i sudjelujete u lutriji!
